Symmetry and Physics
Jan 24, 2021 | 25 min read | casual
Many articles on physics nowadays mention symmetry—supersymmetry, symmetry breaking, symmetry groups, gauge symmetries, CPT symmetry. The term is truly everywhere. In fact, Nobel Laureate Phil Anderson once remarked, “it is only slightly overstating the case to say that physics is the study of symmetry.” For the uninitiated, it is not so obvious what symmetry has to do with physics—however, there are many accessible examples of symmetry at work, perfect for getting a feel for its beautiful ties to the physical world.
What is Symmetry?
We all have some idea of what symmetry means. For example, we would consider a sphere to be more symmetric than a blob, and we are all familiar with the idea of mirror symmetry. The word originates from Greek where it means “agreement in dimensions, due proportion, arrangement,” and sure enough we tend to find symmetry aesthetically pleasing, whether it be in the facial symmetry of an attractive person, or in an intricate pattern such as a Celtic knot.
In physics, symmetry has to take on a mathematical definition for it to be integrated into the rigorous framework of equations. Symmetry of a physical system is defined as the invariance of some physical or mathematical feature of a system under some transformation. By the invariance of a feature, we simply mean that the feature remains unchanged. To put it plainly in the words of mathematician Hermann Weyl, “a thing is symmetrical if there is something you can do to it so that after you have finished doing it, it looks the same as before.”
We can easily relate this definition to the symmetry we are used to. For example, we would consider a square to be symmetric. Specifically, it has mirror symmetries about four axes, and 90 degree rotation symmetries.
In the case of the square, the feature we are considering to be invariant is the orientation and the position of the shape itself. Imagine that you and a friend are in a room, staring at a square piece of paper. After asking your friend to leave the room, you rotate the square by 90 degrees clockwise—this would be what we call a transformation. At the end of this process, your friend returns. Would he be able to tell you “transformed” the square? Assuming the paper is perfectly featureless and you were very careful in rotating the square, he would not be able to. You would have a similar result if you rotated it by any multiple of 90 degrees, clockwise or counterclockwise, or if you flipped the paper along its midlines or diagonals. This is because of the invariance of the position and orientation of the square under these transformations.
We can now also appreciate why a sphere is more symmetrical than an arbitrary blob. A sphere is rich in symmetries—you can rotate it around any axis, by any amount, and it will remain perfectly indistinguishable from its original configuration. Mathematically, the resulting sphere configuration following one of these transformations would be identical to the first. On the other hand, a blob will not necessarily remain invariant under these transformations. If you rotated a banana while your friend was out by less than a full rotation of 360 degrees, he would certainly be able to tell since its orientation would be noticeably different. Orientation? We have actually taken a concept for granted!
What exactly do we mean by orientation in the case of the banana? It can be the direction the stem points, or the direction of a specific discoloration on the banana’s exterior. Notice that we are needing to pick out some distinct feature on the banana to be specific about what we mean by “orientation.” Can we do this in the case of a sphere? No we cannot! The sphere looks exactly the same from any side. We can pick an arbitrary direction as the sphere’s orientation, but if the sphere was just floating in empty space, we would be incapable of explaining this direction to someone else since there is nothing defining a specific direction we can use as a reference. This is an important concept that will return in considering the symmetry of space.
So far we have discussed symmetries that appear in geometry, which is something we are all familiar with. However, we can see that the definition of symmetry in physics is more general than the geometrical notion. For example, consider your social security number as the “feature” we are interested in. If the transformation we are considering is changing jobs, then your social security number can be said to be “symmetric under change of employment”—it does not change when you start a new job. Similarly, your legal name is also symmetric under change of employment. However, it may not be symmetric under the transformation of marriage, for example, since you might choose to take on a new last name after getting married. In physics, many symmetries are like these examples, with no clear connection to geometry. But, as we will see, abstract symmetries share the same powerful insights as the more familiar ones.
Now that we have an idea of what symmetry means to a physicist, we can understand some of the common symmetries in physics.
Physical Symmetries
Some fundamental symmetries considered in physics have to do with transformations that displace physical systems in space and time, as we might expect from a science largely concerned with the motions of objects through time and space.
Imagine empty space, devoid of anything at all, stretching out to infinity in every direction. If you were floating out there in a space suit and your thrusters were to suddenly randomly rotate you this way and that for a long while, completely disorienting you and eventually halting you to face in some direction, you would be incapable of knowing where you were facing relative to before. Just like the case of your friend and the sphere, without any distinguishing feature fixing a direction, there is nothing indicating that anything changed at all. In fact, for all you know you could be facing the exact same direction as before! Just like the case of the sphere, there is nothing that orients space. In fact, it is not just a shortcoming of your own perceptions that makes space look the same in any direction. To physical laws and processes, the only directions that matter are the angles of objects relative to each other within space, and not relative to space itself. For example, if time paused and all the objects in the entire universe were rotated together in space before time restarted, no one would realize that this happened, nor could they find out, even in principle. The stars would still be in exactly the same position in the sky as they were before the rotation, Canada would still be north of the United States, and all the interactions between atoms would continue obeying the exact same laws as before. No experiment would be able to tell us that the whole universe was rotated since as far as we know, the laws of physics cannot be used to define a preferred direction of space, which would allow us to orient it. Every experiment ever conducted has shown no indication that absolute direction matters. Regardless of how an experimental setup is oriented, whether it be an electron diffraction experiment or a human in a clinical trial of a drug, the physical processes progress in the same way. One might argue, “what about a suspended magnetized needle? It would be a compass, and of course the direction it points initially will determine how far the needle swings to eventually point north.” This, while true, still only serves to show that physical processes only care about relative orientations—the relevant orientation here is that of the needle with respect to the earth’s north pole. The earth is part of the physical system in such an experiment, and if the entire system were rotated, including the earth, we would observe the same result as if no rotation transformation were applied. To fully drive the point, if you were to take many exactly identical systems, identical down to the position and velocity of every last particle, and set them up facing different directions in empty space, each system would undergo the exact same time evolution, giving the exact same result in every setup.
So, what we conclude is that the known laws of physics are rotationally invariant, that is, any real physical system and its future evolution remains identical under any arbitrary rotation transformation.
Similarly, the laws of physics are translationally invariant—if time paused and all the objects in the entire universe were shifted together along some direction in space before time restarted, no one would know either. Physics only cares about the relative distances of objects, not about their absolute position relative to space. In fact, just like the problems of orienting a featureless sphere or orienting space brought up earlier, we would not be able to define an “absolute position” in space, just like how we could not define an absolute direction, since no physical process behaves any differently whether it is taking place in one location in empty space or another. On a less grandiose scale, this translational symmetry means that a physical system, say an experimental setup, will evolve the same way whether we start it in Pasadena, in New York, or in Jakarta, provided that the external variables of the experiment are kept unchanged (temperature, local gravitational field, Earth’s magnetic field, etc.), if they are relevant to the processes observed.
$\require{physics}$
Transformations Mathematically
Mathematically, a translation transformation is described by the replacement $\va{r} \to \va{r} + \va{a}$ everywhere where the position variable $\va{r}$ appears in the equations governing the system. The displacement vector $\va{a}$ contains the direction and distance by which the whole system was translated. As an example of applying this replacement, we can turn to Coulomb's law from electrostatics to see that it does indeed remain invariant under translation. Coulomb's law is the equation giving the force between two charged objects carrying charges $q_1$ and $q_2$ located at positions $\va{r}_1$ and $\va{r}_2$, \begin{equation} F = -k_e \frac{q_1 q_2}{\abs{\va{r}_1 - \va{r}_2}^2}, \label{eq:coulombslaw} \end{equation} Where $F$ is the force along the line between the two objects. Applying the translation $\va{r} \to \va{r} + \va{a}$ gives \begin{align} F &= -k_e \frac{q_1 q_2}{\abs{(\va{r}_1 + \va{a}) - (\va{r}_2 + \va{a})}^2}\\ &= -k_e \frac{q_1 q_2}{\abs{\va{r}_1 - \va{r}_2}^2}, \label{eq:samecoulomb} \end{align} which we note is exactly the same equation as before. Hence, we see that Coulomb's law, the physics describing the interaction of two charged objects, is invariant under translation.Now that we are familiar with some of the symmetries of physics in space, we consider the symmetry of physical laws under time translations. Since this idea might sound stranger than the spatial transformations we just discussed, let us return to definitions. The physical or mathematical feature we are interested in is any given physical law in a system, and the transformation we are testing is “pausing” the system, moving it to some other time, then unpausing it. Mathematically, this would be applying the replacement $t \to t + a$ everywhere where the time $t$ appears in the physical equations. For clarity, we should note here that all the transformations we have discussed and will discuss do not actually need to be carried out in reality—for example, we can’t actually apply a time translation to move backward in time, nor would we be able to rotate or displace the entire universe. All that matters is that we can conceive of doing it, that it can be done in our physical equations. That said, we can actually translate a system forward in time to verify this symmetry. A vase falling from a table will break in the same way today as it will tomorrow if it is tipped in exactly the same way. In fact, the entire basis of science rests upon the assumption of time translation symmetry! Time translation symmetry allows us to assume that the physical laws of today are the same as the physical laws of tomorrow, or those of a century ago, or even those of billions of years ago. If the laws of physics changed with time in some arbitrary way (if they changed predictably, the change would just be incorporated into our physical theories and time translation symmetry would still be preserved), there would be no point in studying physics, or doing any science or engineering, for that matter.
However, despite our firm conclusion regarding the presence of time translation symmetry in virtually every physical phenomenon, there is one big anomaly—the Big Bang. Unlike the situation with the breaking vase, or any other physical process, it is not clear what we mean by making the Big Bang happen a day earlier, or a day later. As far as we know, the Big Bang could have been the start of time as we know it, so it might not make sense to even consider translating it in time. Some theories use this as evidence that the universe is an open subsystem: there might be something greater than the universe, a multiverse, for example, in which some process kicked off the Big Bang. In that multiverse, time translation symmetry might be preserved. To relate this to our vase example, if all we knew was the fate of the vase, starting from its tipping to its shattering, we could define all time as starting from the first bit of tilting, since before this, there was absolutely nothing happening. To us, the tipping of the vase inexplicably set forth the arrow of time, ticking forward as ceramic pieces spread farther and farther on the floor. However, what we have not seen is the room the vase was in, where time has always been flowing, and the cat, quickly scampering away after leaning up against an object less stable than she first imagined. From supporting all of science to spawning far-fetched theories about the origin of the universe, as you can start to see, symmetry is intimately connected to many of the most intriguing aspects of physics.
There are many other types of symmetry found in physics. For instance, many physical laws obey time reversal symmetry and describe real physical phenomena even when the direction of time is reversed. Consider a ball thrown straight up in a uniform gravitational field. If we were to record the trajectory of the ball, the motion will appear the same whether the video runs forward or in reverse. The parity transformation, also called spatial inversion, is another transformation under which many physical laws are symmetric. This transformation is mathematically described by $\va{r} \to -\va{r}$, which amounts to essentially a “mirror world.” Studying physical processes that obey this symmetry in a mirror would yield the exact same physical laws. Our earlier example of Coulomb’s law (Eq. \ref{eq:coulombslaw}) is also invariant under spatial inversion, as you can easily check. All of physics was once thought to be parity symmetric. However, in a groundbreaking experiment conducted in 1956 by Chien-Shiung Wu, the weak interaction was found to violate parity symmetry. As seen in the figure below, the beta decay of cobalt-60 was shown to distinguish between left- and right-handed coordinate systems, i.e., between our world and a mirror world.
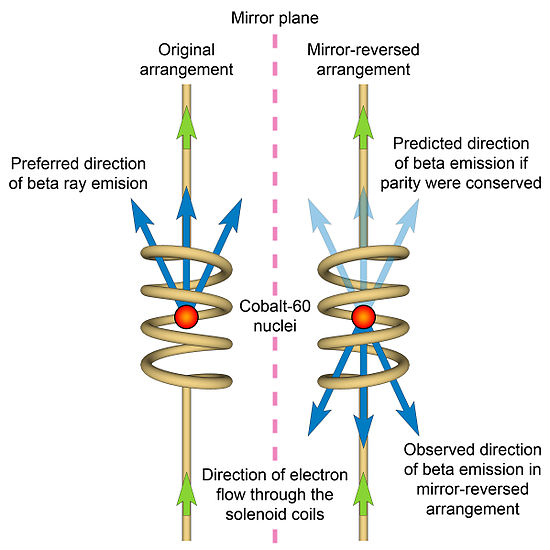
The Wu experiment, showing the parity symmetry violation of the weak interaction. (Wikipedia)
Many crystals remain invariant under glide reflections, a transformation that is composed of a reflection about a line and a translations along that line. For a two-dimensional example, you can imagine looking at a repeated pattern on a wallpaper; the overall pattern looks the same whether you focus on one “tile” or the flipped one next to it.

A ceiling of an Egyptian tomb demonstrating glide reflections. (Wikipedia)
Physicists are also well-versed in more obscure symmetries that require more background to grasp but are ultimately no different in concept than the examples we have discussed. Lorentz transformations are hyperbolic rotations of Minkowski spacetime (the four-dimensional space of our universe, consisting of the three dimensions of space plus the dimension of time) which preserve spacetime intervals, a notion of distance in Minkowski space which is important in special relativity. The Lorentz transformation allows us to go from one frame of reference to another, like if we wanted to see what an experiment on earth looks like if we were in a spaceship speeding past. So, spacetime intervals are symmetric under Lorentz transformations, a property called Lorentz invariance. Electric charge is also a Lorentz-invariant—an observer on earth would agree with another observer travelling at 99.9% of the speed of light blasting by, about how much charge is on a sock fresh out of the dryer. It is because of this invariance that atoms with the same number of electrons and protons are perfectly neutral, despite the electrons whizzing around slow-moving protons. C-symmetry is another interesting topic. C-symmetry is the symmetry of physical laws under a charge-conjugation transformation. That is, you take every positive charge and replace it with a negative one, and vice versa. Referring once again to our fruitful Coulomb’s law example (Eq. \ref{eq:coulombslaw}), we see that replacing $q_1 \to -q_1$ and $q_2 \to -q_2$ results in the same formula as before. In fact, electromagnetism, gravity, and the strong interaction are all C-symmetric, but the weak interactions violate C-symmetry. On a related note, particle physicists call the mirror symmetry we discussed earlier P-symmetry for parity symmetry, and time reversal symmetry T-symmetry. These symmetries can be composed (the associated transformations applied one after the other) to form CP- and CPT-symmetry. CP-symmetry was once thought to be respected by all the laws of physics, both due to theoretical reasons and to the fact that all interactions observed until then agreed with this suspicion, including the Wu experiment we discussed earlier which violates P-symmetry by itself. However, in 1964, James Cronin and Val Fitch found clear evidence proving that the weak interaction could violate CP-symmetry, winning the discoverers the 1980 Nobel Prize. CP violation continues to be a topic of interest due to the matter-antimatter asymmetry we see in our universe. If there was as much antimatter as matter following the Big Bang, (as we would expect, given that in all our experiments which create matter, we unavoidably create an exactly equal amount of antimatter), then where is the entire-universe’s-worth of antimatter that should also be floating around? Currently, the most plausible theories for this missing antimatter require CP violation, so anything learned in this domain will help answer the big questions about why our universe is here in the first place. As we can see, even the lack of symmetry where we expect to find it can be useful, giving you an idea of its importance!
Now we have identified some symmetries, we note that it does provide a nice classification scheme. But, there is so much more! Symmetries help simplify calculations, and even provide guidance for creating new theories for novel physics.
Applying Constraints
Symmetries constrain which theories can be correct, so when physicists find a symmetry that appears to always hold true, it makes it easier to speculate about new theories. As an example, imagine you were asked to draw a curve that finishes where it started. There are many possibilities for what you might draw. However, if you are given the additional constraint that the closed curve is symmetric under any rotation around some point, the required symmetry of the problem heavily constrains what curve you can draw. In fact, the only closed curve that would have this symmetry is the circle.
A similar thing happens in physics. Imagine you have two particles that can interact in some way, as depicted in the example box below. The particles might have various parameters that are relevant to their interaction, including their positions $\va{r}_1$ and $\va{r}_2$. Mathematically and physically, there are six free parameters in just their positions, since each vector $\va{r}$ has three components, $x,y,z$, and each could potentially appear in the function that gives the force experienced by one particle due to the other. But, recall the spatial symmetries we examined earlier. Since the system is composed of just these two particles, if we were to take both of them and shift them somewhere else in space, we would expect the force to be mathematically identical to what it was initially. This means that the position fixing the system in space, say, the position of particle 1, $\va{r}_1$, is irrelevant. Only the relative positions of the two particles can contribute to the force between them. That is, the force is constrained to be a function of $\va{r}_2 - \va{r}_1$. Great, now we are down to just three free parameters that can appear in the force function: $x_{\textrm{rel}} = x_2 - x_1$, $y_{\textrm{rel}} = y_2 - y_1$, and $z_{\textrm{rel}} = z_2 - z_1$. Let us also invoke the rotational invariance of physical laws. If we were to rotate the whole system in empty space by some angle, it will not change the physics between the two particles either. So, for convenience, consider rotating the system about the position of particle 1, $\va{r}_1$. This changes the direction of particle 2 relative to particle 1, and we know that this cannot change the physics. Hence, only the relative distance between the particles can matter! This means that the only term that can appear in the force function is a single parameter, $\abs{\va{r}_2 - \va{r}_1}$, the distance between the two particles.
Applying Constraints to Simplify a Problem
Just like that, we have collapsed six variables into one through the constraints imposed by the symmetry of the system. Notice that our favorite, though now overused, example, Coulomb’s law (Eq. \ref{eq:coulombslaw}), is also concerned with the force between two particles. Sure enough, we see that neither $\va{r}_1$ nor $\va{r}_2$ appear by themselves in the equation—only the relative distance $\abs{\va{r}_1 - \va{r}_2}$ does. This simple example shows the logic theoretical physicists use when formulating new theories, after assuming which symmetries might be obeyed by the novel phenomena.
Reasoning by Symmetry
Symmetry can also be used to drastically simplify calculations when we know the physical laws governing a process. Often, these shortcuts arise when we are trying to “complete” a system, whether we know the shape of an airplane and want to know the airflow around it, or if we know the distribution of charge on an object and want to find the electric field surrounding it. The part we are trying to complete usually “mirrors” the symmetry of the part we know, especially when the part we know is the “source”. For example, in the case of the airplane, the deviation of the airflow is due to the shape of the airplane, which has mirror symmetry down its middle. Hence, we would expect the airflow about the left wing to look like the mirror image of the airflow about the right wing. A similar copying of symmetry happens for the electric field surrounding a charged object. When the source is symmetric in many ways, the electric field can almost be completely determined. As before, when we are trying to think of an object with many symmetries, the sphere comes to mind. In the case of a sphere carrying a uniform distribution of charge, we can deduce a lot about the electric field just through considerations of symmetry. In the following example box, we will reason our way to the electric field surrounding a charged sphere.
Electric Field Around a Charged Sphere
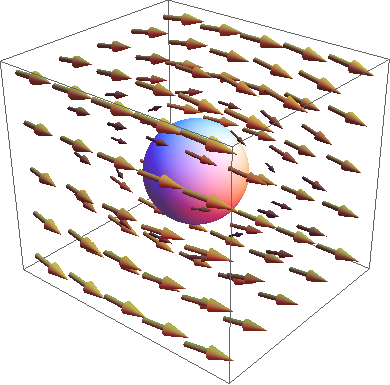
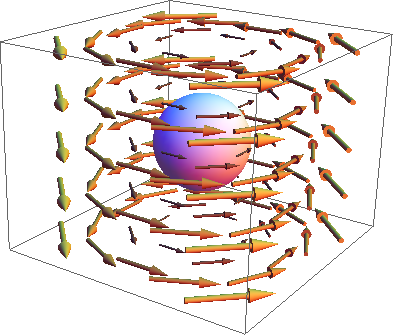
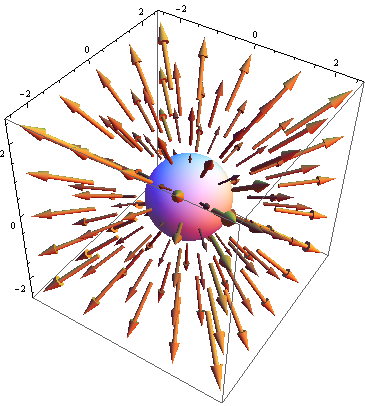
Let us use symmetry to figure out the electric field surrounding a charged sphere. As a testament to how powerful symmetry is, you do not even need to know anything about what an electric field is, aside from the fact that it consists of vectors, at every point in space, of some magnitude pointing in some direction. In all the following figures, you have to fill in the blanks with your mind, since the arrows are only drawn at some points to give an idea of what the field looks like, while in reality they exist at every point. In our quest to find the electric field, the name of the game is to mirror the symmetry of the source, which in this case has spherical symmetry. Consider the following guesses for what the electric field looks like: Let us examine the first guess for the electric field. Does the field copy the symmetry of the source? No, since if we are to rotate the sphere, it would look exactly the same, but it is clear that rotating this electric field produces an obvious difference in the direction of the vectors. Such a field would beg the question, what is so special about the direction in which all the arrows appear to be pointing? Considering our discussion about the rotational symmetry of space, such a distinct direction should not exist. Since our sphere does not break rotational symmetry, it cannot specify a unique direction either. Hence, we cannot have the electric field in the first image. What about our second guess? Here we do not see as obvious of a direction being pointed out. However, note that if you were to flip the sphere upside-down, the arrows would spiral in the other direction, even though the source would look exactly the same. Therefore, this cannot be the electric field either. Finally, consider the last proposed electric field. Imagine rotating the sphere in any which way—the field still looks the same! This looks promising; it obeys the symmetry dictated by the source. In fact, you can convince yourself that only two configurations will respect the symmetry of the system: the one shown with arrows pointing outward, and a similar field with all the arrows pointing inward. Both of these configurations are actually the only permissible electric fields for this charge setup! When the sphere is positively charged, the arrows point outward, and when it is negatively charged they point intward. We almost know everything there is to know—at this point we would just need to determine the magnitudes of the electric field vectors at various distances from the center of the sphere, which can easily be accomplished using Gauss's Law.As seen in the example of a uniformly-charged sphere, symmetry reasoning did almost all the work of determining the electric field for us, and we did not have to use any physics until the last step. This is one of the many beauties of symmetry.
Noether’s Theorem
One of the most astounding results of symmetry is Emmy Noether’s theorem. This mathematical theorem has become one of the fundamental tools of modern theoretical physics, and is worthy of being called the crown jewel of symmetry. The theorem can be stated informally as “if a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time.” To understand what is being said here, let us break down each part of the theorem and explain the terminology.
A continuous symmetry is defined by a property of its transformation. A continuous symmetry is associated with a transformation that can be applied infinitesimally, that is, a transformation that can be broken into many smaller ones each of which are arbitrarily close to doing nothing. For example, spatial translation is a continuous symmetry since you can translate a system by a vanishingly small amount. Such a transformation is infinitely close to the identity transformation, the transformation of doing nothing at all. Compare this to a non-continuous, discrete symmetry such as time reversal symmetry. The time reversal transformation is not continuous since you cannot decompose it into vanishingly insignificant transformations that are close to the identity transformation—either you reverse the arrow of time, or you do not. To give a few more examples, spatial rotation and time translation are other continuous symmetries, while charge conjugation and parity transformation are discrete symmetries. You can rotate a system by a tiny amount, but you cannot flip the signs of all electric charges by a tiny amount.
So, assuming that a system has a continuous symmetry, Noether’s theorem says that there is an associated conserved quantity. Conserved quantities give rise to conservation laws, a concept explored early on in introductory physics and engineering courses. You are probably familiar with the conservation of linear momentum, for example, and if you have used it before, you know how incredibly useful it can be in carrying out physical calculations. It turns out that the conservation of linear momentum is mathematically implied by spatial translation symmetry! This is truly astounding—the quantity that Newton long ago noticed stays the same in every closed system, is simply a consequence of the fact that the system behaves the same way whether it is performed here, or a few centimeters to the left, right, up or down! Naturally, now you are probably wondering what symmetry is linked to the conservation of energy, the other immensely famous conservation law of physics. Energy conservation is tied to time translation symmetry—a physical system that undergoes the same processes whether it is started now, a few seconds ago, or a year into the future will conserve its total energy. What happens when a symmetry is broken? For example, earlier we discussed how the Big Bang breaks time translation symmetry. If a symmetry is broken, its associated quantity does not need to be conserved! So, considering the colossal amount of mass and energy released during the Big Bang, presumably from nothing at all, and how this event violates time translation symmetry, we find that these occurrences go hand-in-hand.
Below we have a table with some of the more well-known Noether symmetries and associated conservation laws.
Fundamental Symmetries and Associated Conserved Quantities
| Symmetry Invariance | Conservation Law |
|---|---|
| time invariance | mass-energy |
| translation symmetry | linear momentum |
| rotation invariance | angular momentum |
| Lorentz invariance | CPT symmetry |
| $\textrm{U(1)}_\textrm{EM}$ gauge invariance | electric charge |
| $\textrm{SU(3)}$ gauge invariance | color charge |
| $\textrm{SU(2)}_\textrm{L}$ gauge invariance | weak isospin |
| probability invariance | probability |
Now we can see one big reason physicists are so interested with symmetry—finding a new symmetry could mean a new conservation law.
Ave Symmetry
Now I hope you have an increased appreciation of the close ties between physics and symmetry, and a little extra insight into why physicists would ever want a spherical cow. Many beautiful results in physics are intimately related to symmetries, which serve to simplify, guide, and predict. Perhaps this is one reason humans find symmetry so beautiful; it governs much of the world around us, as well as within us.
Cover image: Big European Bubble Chamber (cern.ch) and ceiling of an Egyptian tomb (wikipedia.org).
I originally wrote this article for Ph70, Oral and Written Communication (of Physics), at Caltech.