Neural Stack Implementation

Dec 22, 2019 | 7 min read | technical

I implemented and successfully trained DeepMind’s Differentiable Neural Stack from scratch using PyTorch, resulting in one of the first publicly available PyTorch implementations of a neural stack, appearing on Papers with Code.

Based on “Learning to Transduce with Unbounded Memory” by Edward Grefenstette, Karl Moritz Hermann, Mustafa Suleyman, Phil Blunsom. (arXiv)

This work was part of an assignment in CS281: Advanced Machine Learning at Harvard in 2019, and I was the only one in a class of around 200 students to successfully make it work.

Neural Stack Architecture

A stack is a last-in-first-out (LIFO) data structure that is used in many algorithms to handle recursion, nesting, or simply to reverse sequences of data. Incorporating such a system into a neural network would be helpful for a multitude of tasks as it allows for leveraging a stack’s properties and to grant the network access to an effectively unlimited data storage capacity. DeepMind’s innovation was making a classical stack’s operations differentiable, such that a neural network could learn to control it through backpropagation, and allowing for embedded states to be used as its elements. In brief, this is accomplished by allowing for a superposition of element presence within the stack, controlled by a “partial” application of push and pop operations. A careful explanation can be found in their paper.

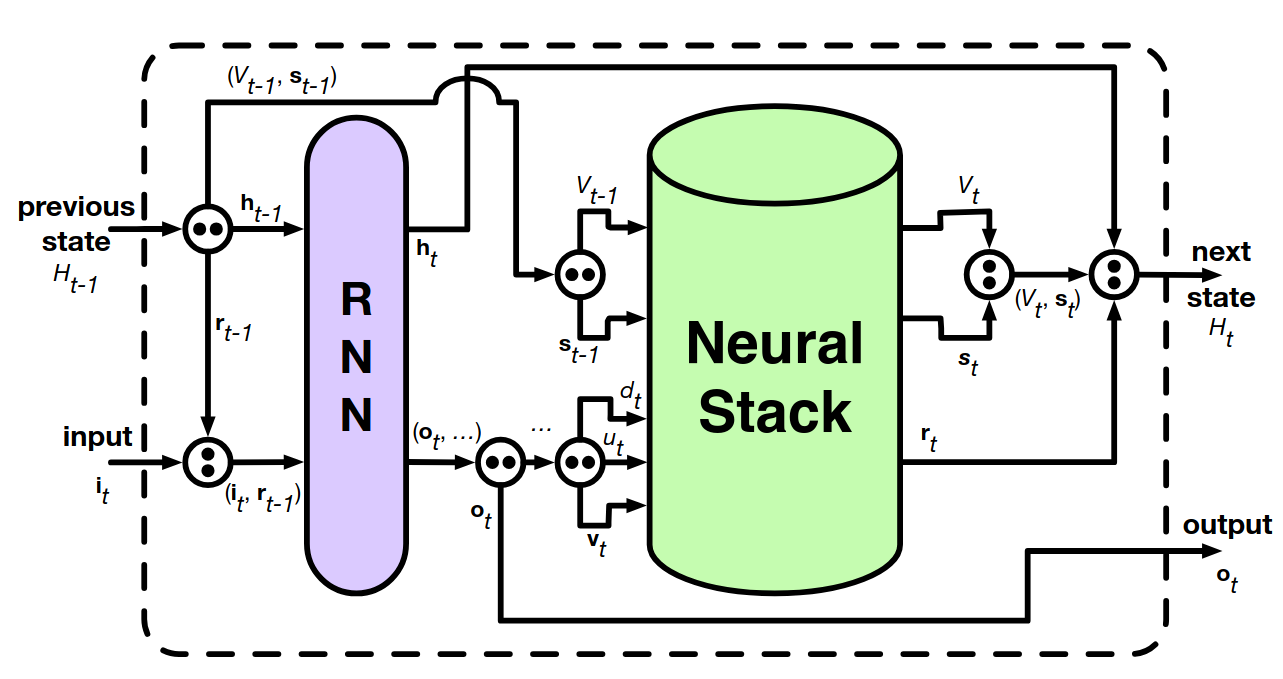
$Figure 1. [From Learning to Transduce with Unbounded Memory]. (a) shows how elements within the neural stack have a fractional presence, and (b) depicts the neural stack’s recurrence unit. The final schematic (c) shows the full recurrence unit where an RNN controlling the neural stack.$

Figure 1. [From Learning to Transduce with Unbounded Memory]. (a) shows how elements within the neural stack have a fractional presence, and (b) depicts the neural stack’s recurrence unit. The final schematic (c) shows the full recurrence unit where an RNN controlling the neural stack.

Experiment

After completing a vectorized implementation of the neural stack for efficiency, I tested it using a simple generalization experiment. I trained a multi-layer vanilla RNN, LSTM, and LSTM with a neural stack to reverse an input sequence of characters. Strings in the training data had lengths between 8 and 64 characters, while the test set had strings of lengths 65 to 128. This crucial distinction between the training and test sets gauged the generalizability of the network on this task as the test distribution was entirely disjoint from the training distribution. In order to perform well on the test set, the networks would actually need to learn the concept of reversing a sequence instead of emulating its effects on similar data.

For an example of the input and target data, let $ be the start character, | be the separator, and & be the termination character. Given the input:

$A string to reverse|

the expected output would be:

esrever ot gnirts A&

During training, strings within the length constraint were generated randomly, spanning a space of $10^{135}$ possible training sequences, so in practice “infinite” data was available and overfitting is impossible with the network sizes tested.

I tested standard recurrent neural networks (Elman RNN and LSTM) as a baseline for this task, compared to an LSTM connected to the differentiable neural stack. All the operations in the stack are differentiable, allowing for standard cross-entropy loss minimization through backpropagation to train the neural network to use the stack in a way it finds useful, storing encoded information of its choice in the data structure.

While using such an architecture to reverse strings is an academic example, as noted in the original paper the ability to reverse information, or to store it away for later use, is a very powerful addition to neural networks. Without needing to specify how these data structures are to be used in a given task, a network can learn to best leverage them. For example, when translating between languages, there are often reorderings of parts-of-speech where a stack could be helpful. While standard RNN approaches have been shown to work for these tasks, they fail to consistently generalize to strings longer than those seen in training. The logically unbounded memory offered by a neural stack solves the issue with long-range reorderings.

Results

The performances of the RNN, LSTM, and LSTM + Neural Stack models were tested on fixed validation data (using strings of the same length as in training) and test data (using strings strictly longer than those used in training, guaranteeing that they were not seen).

The performance was evaluated using “coarse” and “fine” accuracy scores defined as

$$\textrm{coarse} = \frac{\#\textrm{correct}}{\#\textrm{seqs}}, \qquad \textrm{fine} = \frac{1}{\#\textrm{seqs}} \sum_{i=1}^{\#\textrm{seqs}} \frac{\#\textrm{correct}_i}{\left|\textrm{target}_i\right|}$$

where $\#\textrm{correct}$ and $\#\textrm{seqs}$ are the number of correctly predicted sequences (in their entirety) and the total number of sequences in the validation/test sets, respectively. In the fine metric, $\#\textrm{correct}_i$ is the number of correctly predicted characters before the first error in the $i$ th sequence of the validation/test set, and $\left|\textrm{target}_i\right|$ is the length of the test segment in that sequence. Essentially, the coarse accuracy is an “all or nothing” measure, not giving any partial credit, while the fine accuracy gives partial credit for reversals that are correct up to a point.

Best Models

The fine accuracy results for the best RNN, LSTM, and LSTM + Neural Stack models are shown below. I performed hyperparameter searches across the size of the hidden state, learning rate, optimizer, number of stacked RNN/LSTM layers, and embedding size to arrive at these top-performing models.

Figure 2. The selected best models from the RNN, LSTM, and LSTM + Neural Stack architectures. On the top left, we show the validation accuracy of these three models against the batch number. The validation set only consists of sequences between 8 and 64 characters long, the same distribution as the training data. Notice that the RNN and LSTM models eventually achieve decent performance on this task, though even after 100x more data than seen by the neural stack they still cannot match its performance. On the top right show the remarkable generalization of the neural stack on the test data, consisting of sequences of 65 to 128 characters. Notice that once the neural network figured out how to achieve perfect accuracy on the training data, it simultaenously figured out how to achieve perfect performance on the longer sequences that were never seen during training. In contrast, the RNN and LSTM do not achieve acceptable performance. On the bottom we show the loss curves for the three models during training.

Notice that the Neural Stack achieves perfect reversals even on the test set, while the RNN and LSTM models have significantly worse accuracy on these longer strings.

Looking at coarse accuracy, we see that the RNN and LSTM networks could not successfully reverse a single string from the test set in its entirety!

Figure 3. The neural stack is able to achieve perfect performance on both the validation and test sets while the RNN and LSTM cannot accurately reverse a single sample.

Neural Stack Training Consistency

I did observe some dependence on the random initial weights, indicating some fussiness in getting the neural stack setup to work. Most of the time, the LSTMs with neural stacks would eventually figure out how to properly use them, but about a third of the the networks settled towards the wrong regions of parameter-space where the stacks were not used effectively, as shown by the consistency plots below.

Figure 4. Consistency of training for the same architecture and training hyperparameters but with different randomly initialized starting weights. Not all networks figured out how to use the neural stack appropriately.

In these identical runs with different weight initializations, 2 of 6 runs did not learn to use the stack correctly. However, even if a real application involving these stacks may have to be trained a few times before it takes, it could end up being worth it if using a stack could help achieve perfect accuracy on some subtasks.